Формули, що необхідно знати на ЗНО з математики 2023

Хочете краще та ефективніше підготувати учня до ЗНО з математики? Ми зібрали усі найважливіші формули, що будуть на цьогорічному тесті: від теорії ймовірностей до тригонометрії.

Неможливо добре підготуватися ЗНО з математики, не запамʼятовуючи основні формули. Вони знадобляться для вирішення більшості завдань в тесті. Однак, щоб запамʼятати їх всіх, матеріал потрібно часто повторювати. Не забувайте, що чітка структура вибудовується на розумінні усіх тем, які будуть представлені у тесті та підготовці до ЗНО з репетитором з математики. Збережіть цю статтю, як шпаргалку, та повертайтесь до неї, якщо буде потрібно. Спробувати усі ці формули в дії можна під час безкоштовного курсу по ЗНО з математики. А, щоб перевірити свої знання спробуйте демонстраційний НМТ з математики від Mathema.

Підготуйтесь до ЗНО/НМТ разом із репетитором

Найкращий спосіб засвоїти усі теми ЗНО та НМТ з математики — скористатися послугами репетитора. Професійні педагоги допомагають заповнити пробіли в знаннях учня та освіжити в памʼяті шкільну програму. В онлайн-школі Mathema учень може пройти курс повної підготовки до НМТ з математики і отримати хороший бал на тестуванні. Дізнатись більше можна за посиланням нижче.

Формули з алгебри та початку аналізу для ЗНО

Формули скороченого множення

Ці формули дозволяють виконати множення многочленів простіше. Формули для квадратів використовують частіше за інших і починають вивчати ще у сьомому класі.

Модулі

Запамʼятайте три важливі правила про модульні числа: модуль числа не може бути від’ємним; модуль додатного числа та нуля дорівнює самому числу; модуль від’ємного числа дорівнює протилежному числу.

Степені

Формули степенів потрібні для спрощення складних виразів при розв’язанні рівнянь та нерівностей.

Квадратні рівняння

Квадратне рівняння можна розв’язати за допомогою процедури розкладання на множники та за допомогою дискримінанта. Дискримінант дорівнює різниці квадрата другого коефіцієнта і добутку першого коефіцієнта та вільного члена, помноженого на чотири. Дискримінант позначається великою латинською буквою D.

Логарифми

Це число, яке показує, до якого степеня потрібно піднести “а”, щоб отримати “b”. Основні властивості логарифмів описуються формулами.

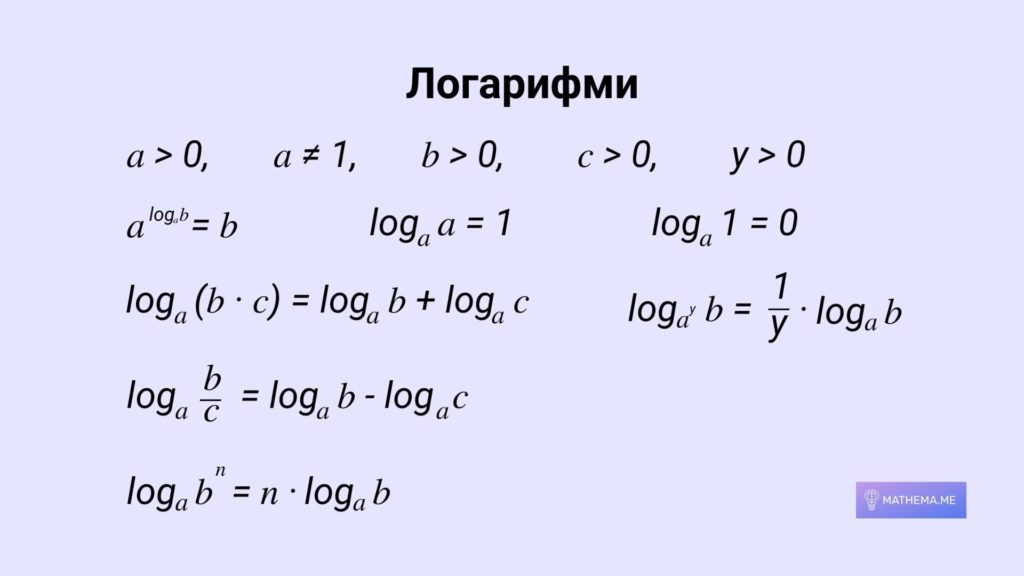
Читайте також: Як впоратись із тривогою і не хвилюватися перед ЗНО чи НМТ

Прогресії

Арифметична прогресія

  Це послідовність дійсних чисел, кожен член якої, починаючи з другого, утворюється додаванням до попереднього члена одного й того ж числа. Наприклад “2, 4, 6, 8…”. 

Геометрична прогресія

Тут кожен наступний член прогресії множиться на число. Наприклад, якщо послідовність степенів “2”, то геометрична прогресія виглядатиме так: “2, 4, 8, 16”. 

Теорія ймовірностей та комбінаторика 

Цей розділ вивчає закономірності випадкових явищ: випадкові події, випадкові величини, їхні функції, властивості й операції над ними. У визначенні ймовірностей допомагає комбінаторика.

Функції

Похідна функції

Похідна — поняття диференціального числення, що характеризує швидкість зміни функції. Вона визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля.

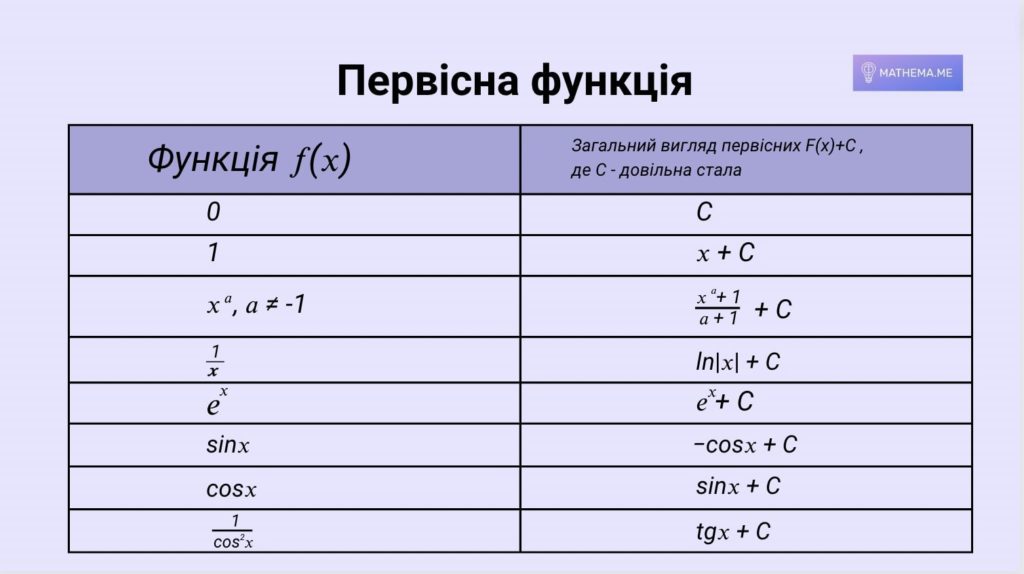
Первісна функція

Функція називається первісною на проміжку, якщо для будь-якого з x з цього проміжку F‘(x) = f(x).

Читайте також: Як підготуватися до ЗНО з математики: детальний гайд

Тригонометрія

Цей розділ лежить на перетині алгебри та геометрії та вивчає співвідношення між сторонами й кутами трикутників. Тригонометрія дозволяє проводити кутові обчислення через спеціально визначені функції кутів.

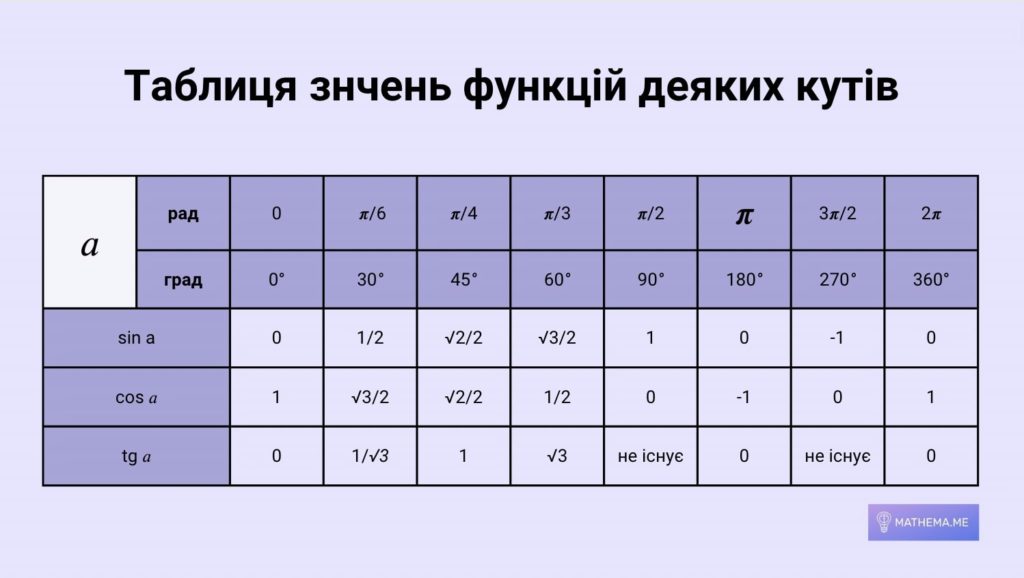
Таблиця значень функцій деяких кутів

Це записані в таблицю пораховані значення синусів, косинусів і тангенсів кутів від 0° до 360°.

Формули з геометрії для ЗНО з математики

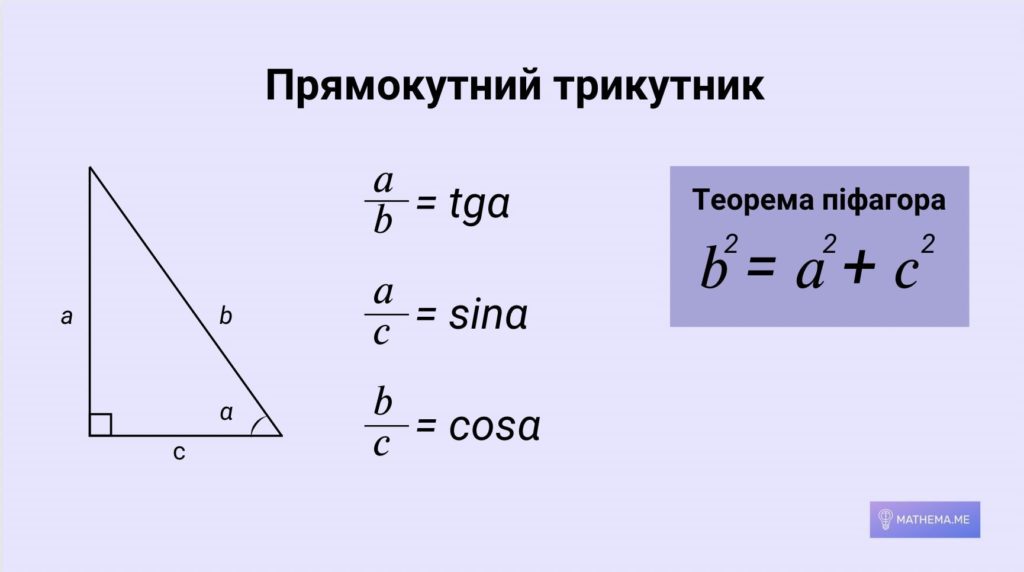
Трикутники

Трикутник — фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно з’єднують ці точки. Точки називають вершинами трикутника, а відрізки — його сторонами.

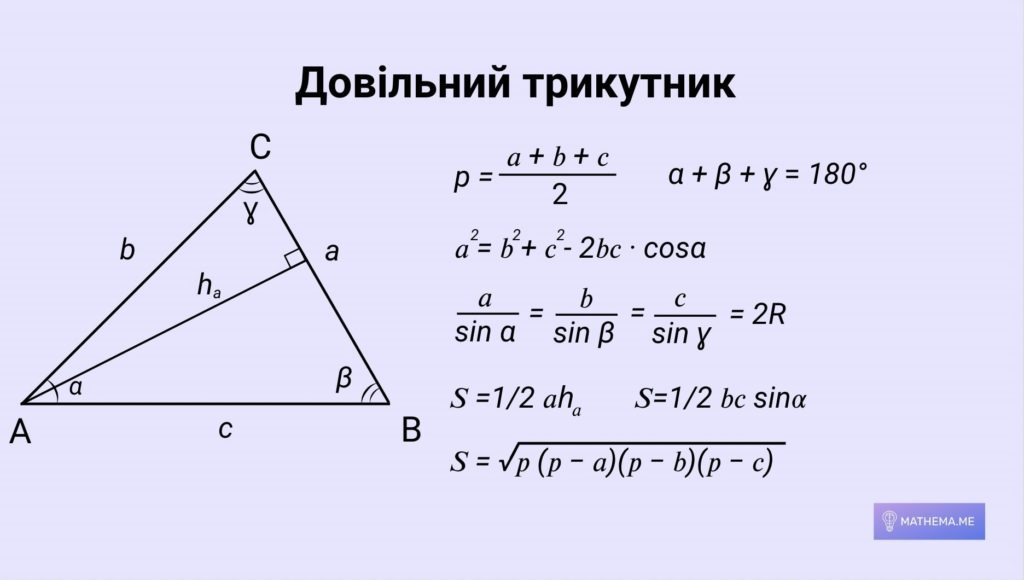
Читайте також: Формули для НМТ, яких не буде в довідкових матеріалах. Що потрібно знати

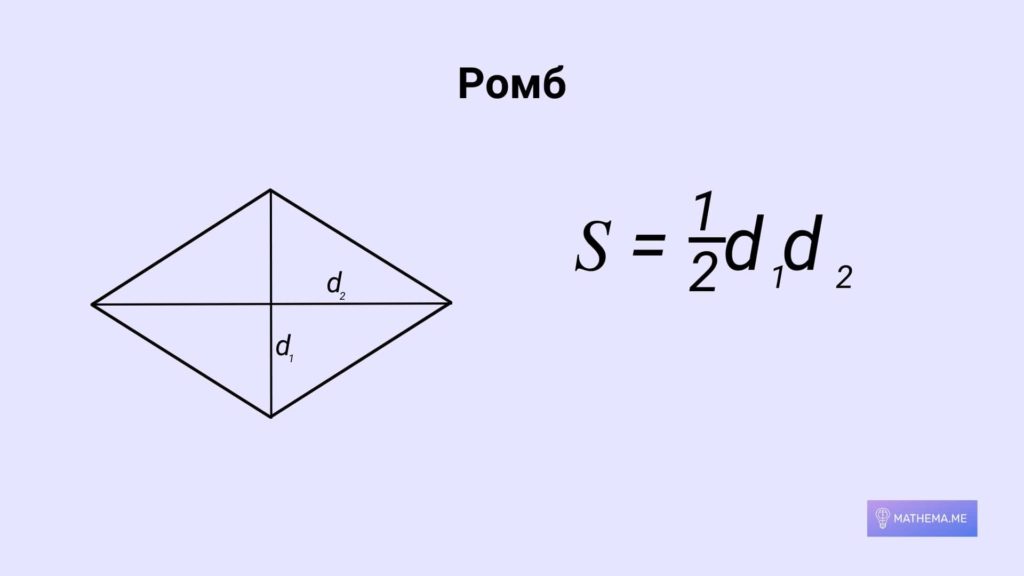
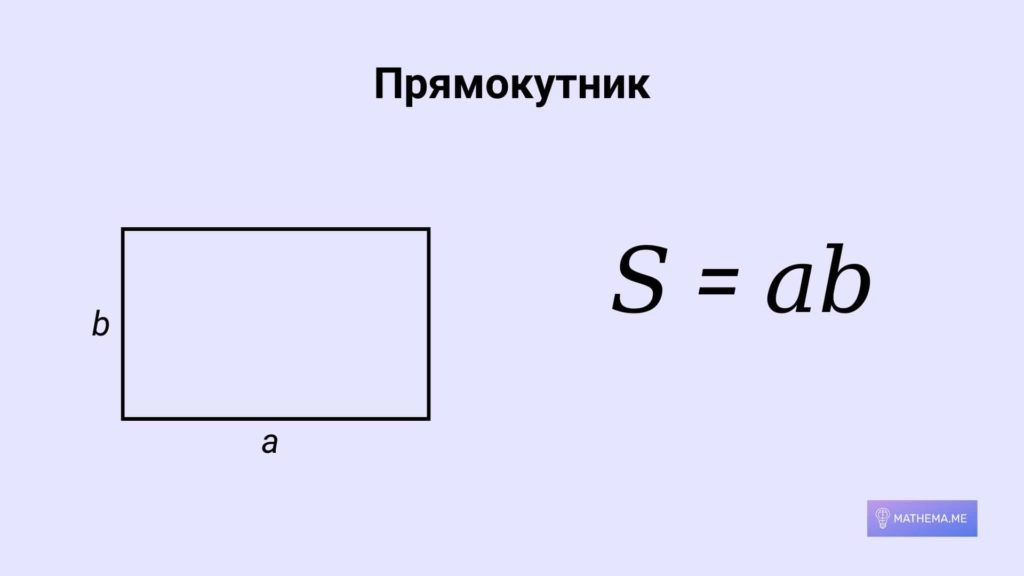
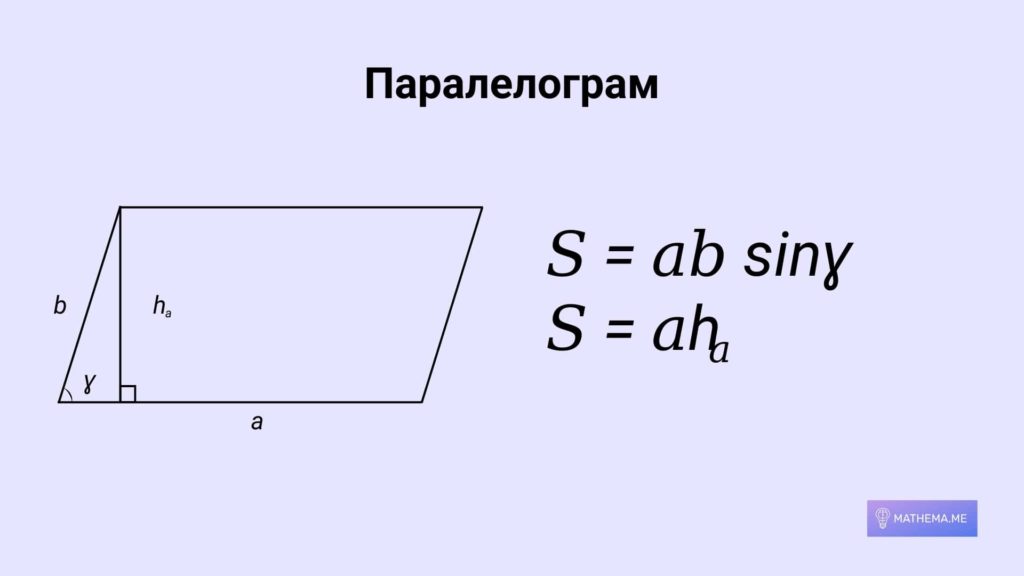
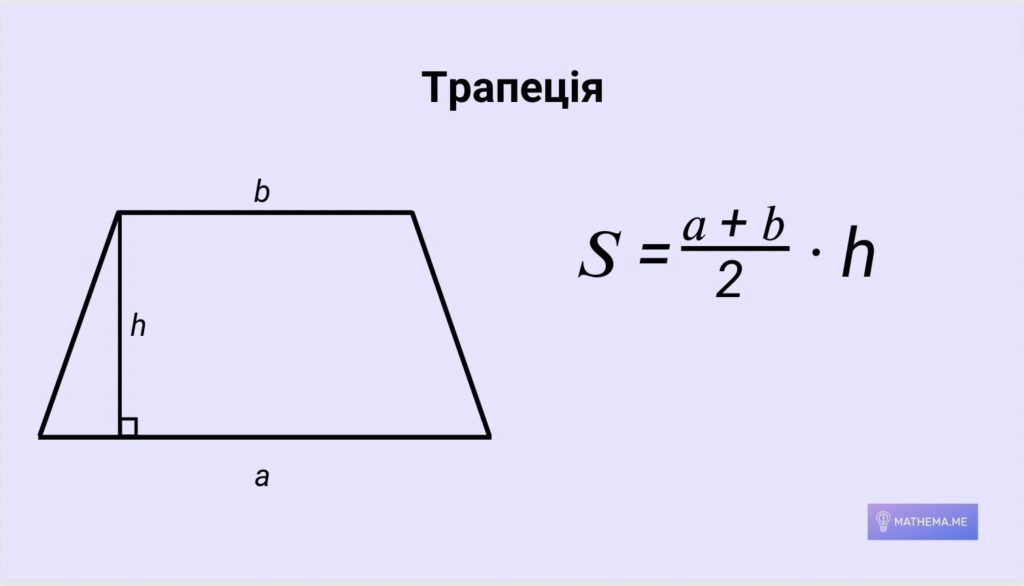
Чотирикутники

Чотирикутник — це багатокутник з чотирма вершинами, три з яких не лежать на одній прямій. Площа чотирикутника може бути задана за допомогою тригонометричних функцій. 

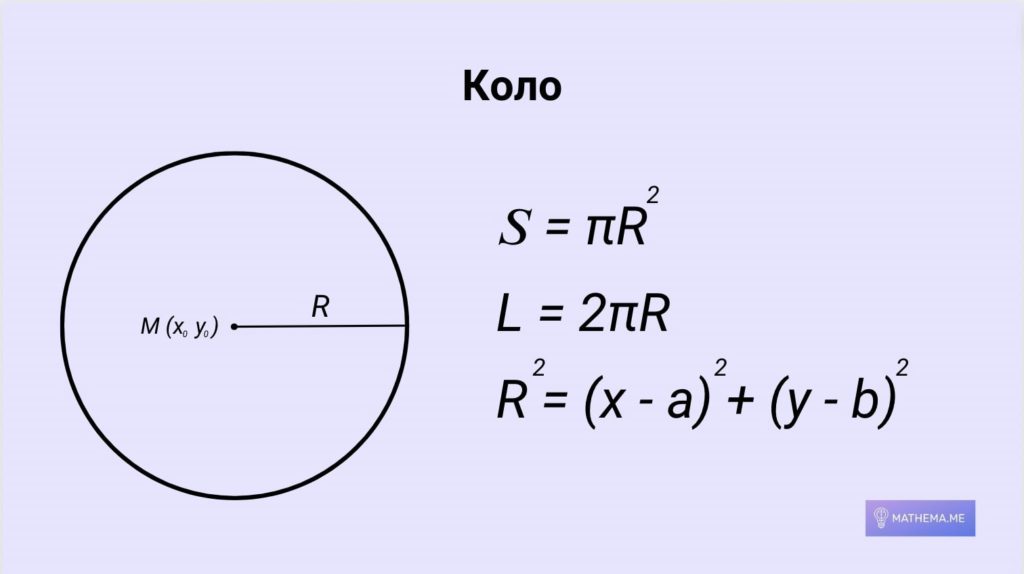
Коло і круг

Коло — це сукупність усіх точок на площині, які знаходяться на однаковій відстані від заданої точки, яка називається центром кола. Діаметр кола дорівнює двом радіусам.

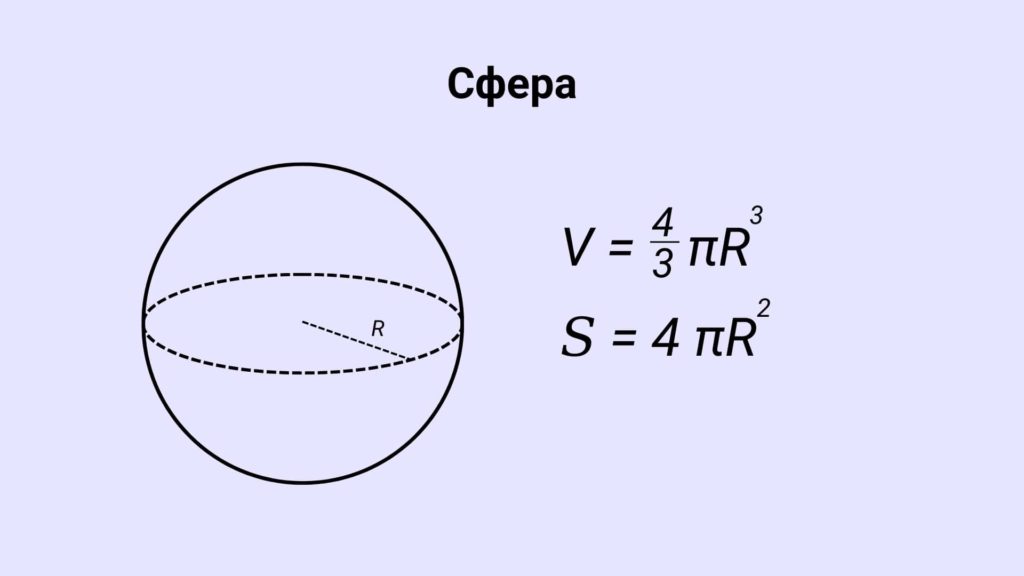
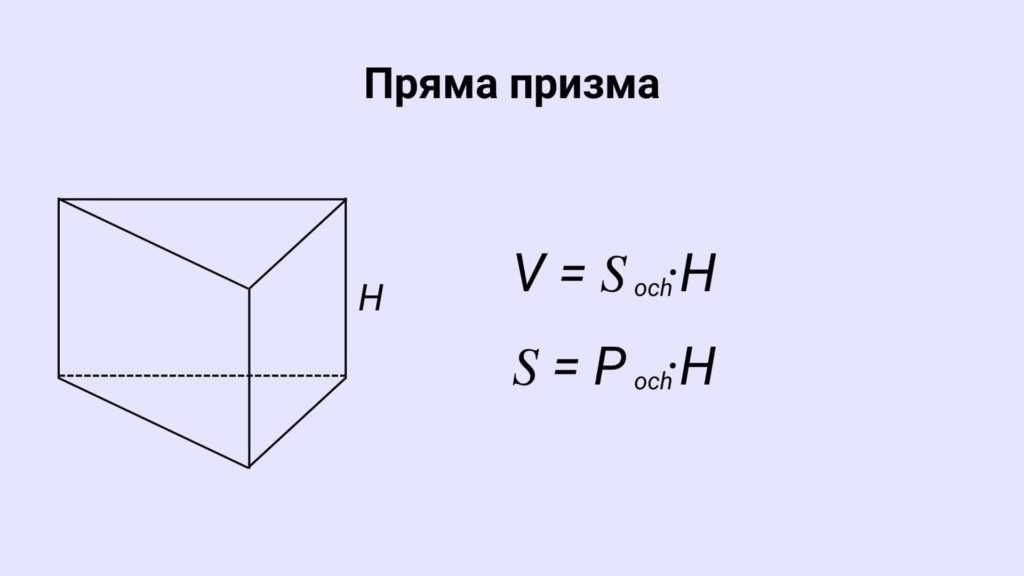
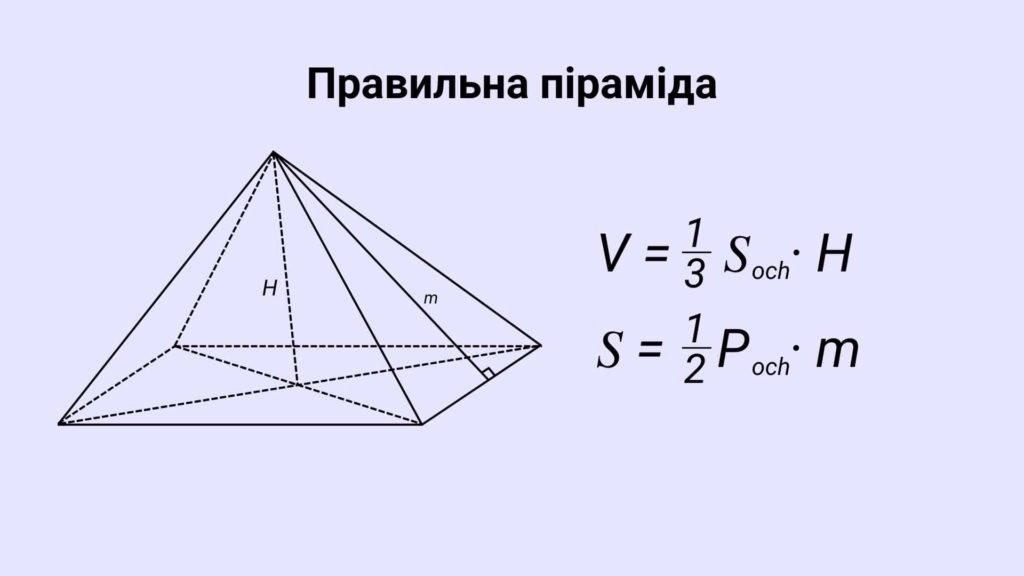
Обʼємні фігури та тіла

Обʼємні фігури займають розташовані у трьохвимірній площині. Хоча для зручності їх зображають у двовимірному виді, заштриховуючи лінії, які не видно в реальності.

Координати та вектори

Вектором називається спрямований відрізок. Координатами вектора є координати кінцевої точки цього вектора, якщо вектор розташований так, що його початок знаходиться на початку координат.