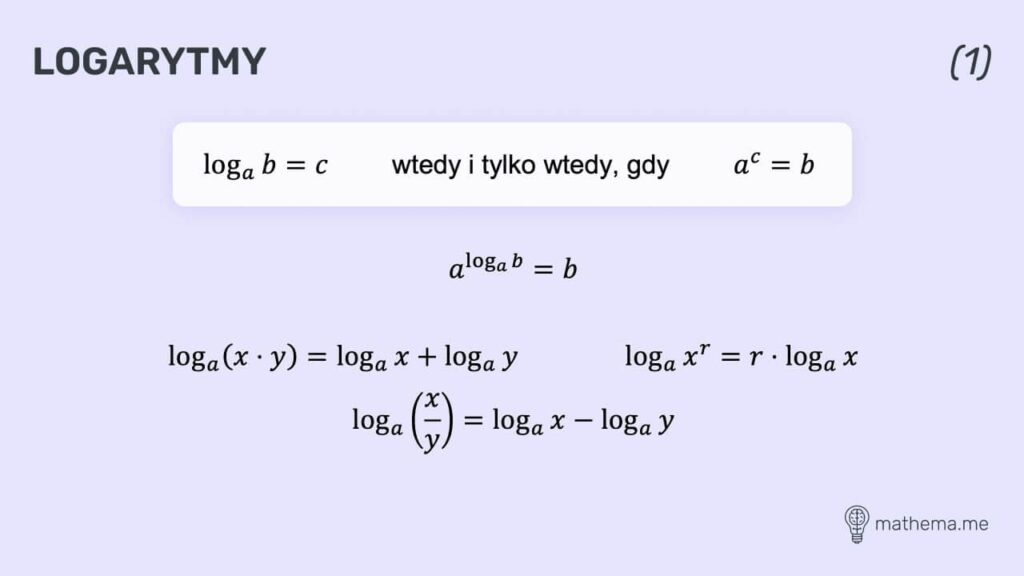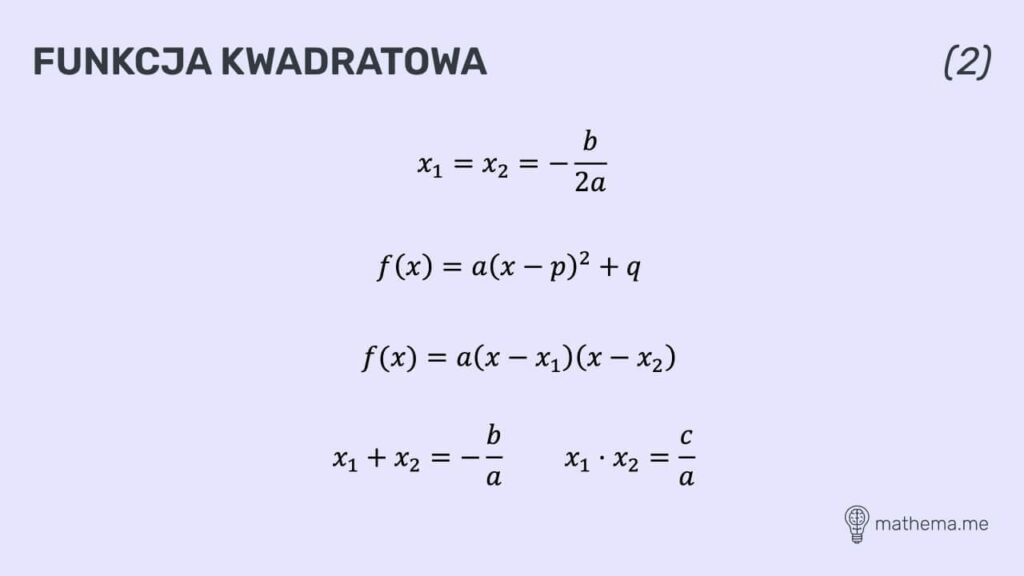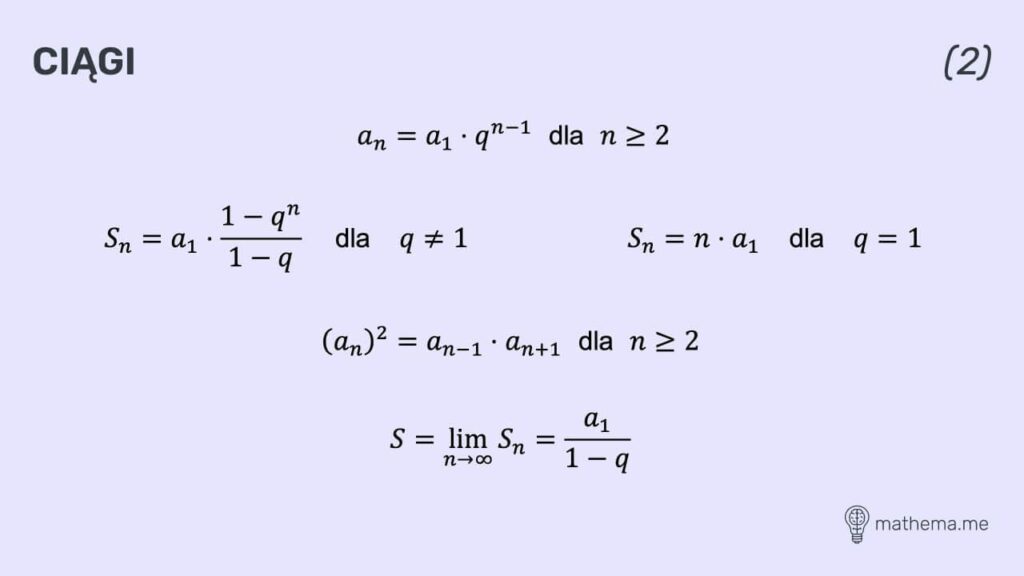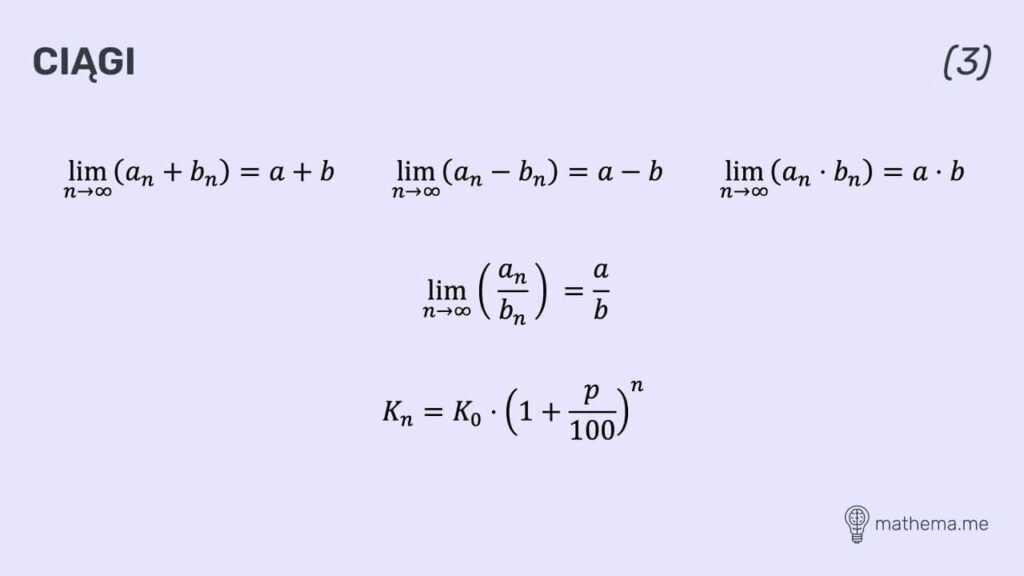Wzory na egzaminie maturalnym: co musisz wiedzieć?

Szukasz informacji na temat: wzory matematyczne matura? Chcesz zrobić sobie powtórkę z wszystkich ważnych wzorów matematycznych? Przeczytaj artykuł Internetowej Szkoły Mathema i dowiedz się jakie wzory musisz znać na egzaminie maturalnym zarówno na poziomie podstawowym, jak i rozszerzonym.

Wzory umożliwiają rozwiązywanie wielu zadań matematycznych. W artykule przygotowanym przez Internetową Szkołę Mathema zostały zestawione najważniejsze wzory matematyczne potrzebne na maturze. 

Jakie wzory matematyczne na maturze 2023? Wszystkiego dowiesz się czytając poniższy artykuł. Znajomość wzorów jest często niezbędna w rozwiązywaniu zadań, chociażby obliczenie pola czy objętości figur geometrycznych jest możliwa właśnie dzięki nim. Warto więc zapisać sobie ten artykuł i wracać do niego w razie potrzeby, ponieważ zawiera on odpowiedź na często wyszukiwane pytanie — jakie są najważniejsze wzory matematyczne matura?

Wartość bezwzględna liczby

Warto zacząć od wzoru na wartość bezwzględną liczby. Określa on odległość tejże liczby od zera na osi liczbowej. Na przykład, wartość bezwzględna liczby -5 wynosi |-5|= -(-5) = 5, ponieważ -5 jest oddalone od zera o 5 jednostek na osi liczbowej. 

Wzór na wartość bezwzględną liczby używany jest w wielu dziedzinach nauki. W matematyce wykorzystywany jest przede wszystkim do obliczania odległości między dwoma punktami na osi liczbowej, a także do rozwiązywania równań oraz określania wartości minimalnej lub maksymalnej.

Potęgi i pierwiastki

Najprościej mówiąc, potęga to liczba powstająca w wyniku mnożenia liczby przez samą siebie wiele razy. Patrząc na wzór można zauważyć podstawę potęgi (a), którą się mnoży oraz wykładnik potęgi (n), który określa ile razy należy pomnożyć podstawę przez samą siebie. Z potęgami można się spotkać we wzorze na obliczenie pola kwadratu, gdzie długość boku a podnoszona jest do potęgi 2.

Pierwiastek n-tego stopnia z liczby a to taka liczba, która po podniesieniu do potęgi n daje wynik a. Zastosowanie pierwiastków można zauważyć na przykład w geometrii czy podczas rozwiązywania równań kwadratowych.

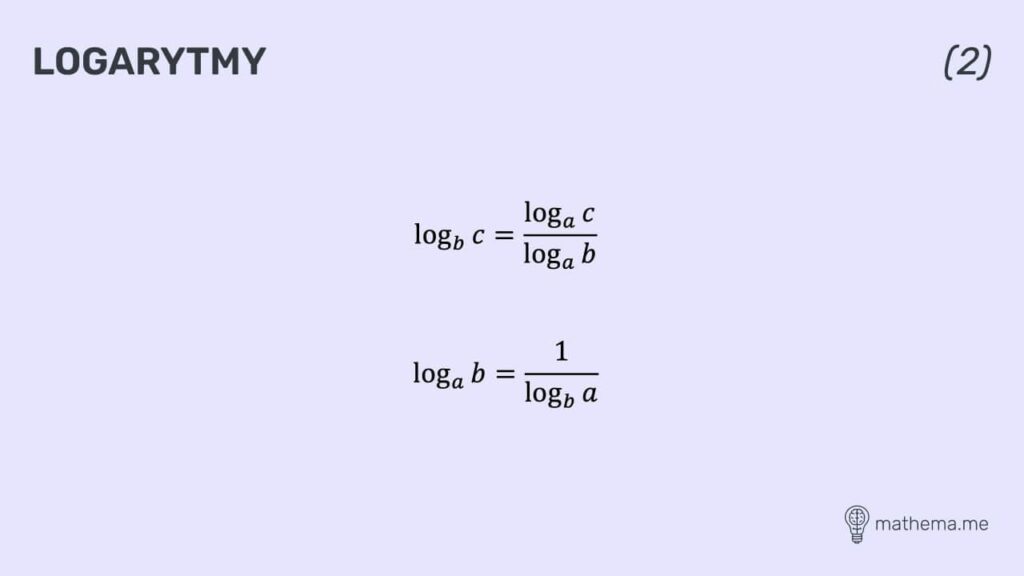
Logarytmy

Jednym z podstawowych działań w matematyce są logarytmy, dzięki którym możliwe jest przekształcanie działań mnożenia i dzielenia na dodawanie i odejmowanie. Najprościej: logarytmy to odwrotność potęgowania. Na podstawie wzoru, logarytm liczby b przy podstawie a to taka liczba c, że a podniesione do potęgi c daje liczbę b.

Znajomość logarytmów przydatna jest w operacjach związanych z liczbami o bardzo dużej lub bardzo małej wartości. Skomplikowane operacje matematyczne są możliwe do wykonania w postaci prostych działań dodawania lub odejmowania. 

Silnia. Współczynnik dwumianowy

Silnia istotna jest w kombinatoryce, dlatego warto być zaznajomionym z poniższym wzorem. Najogólniej silnia to funkcja matematyczna, która dla danej liczby naturalnej n określa wynik mnożenia wszystkich liczb naturalnych mniejszych lub równych n. Oznacza się ją wykrzyknikiem (!), który stawiany jest po liczbie, dla której obliczana jest silnia. 

Jeśli chodzi o współczynnik dwumianowy, to jest to liczba, która określa liczbę możliwych podzbiorów składających się z k elementów wybranych spośród n elementów. Współczynnik dwumianowy przydatny jest w kombinatoryce oraz prawdopodobieństwie, ponieważ może posłużyć do ustalenia liczby możliwych wyników losowań czy kombinacji. 

Wzór dwumianowy Newtona

Jest to twierdzenie nazwane na cześć matematyka Isaaca Newtona. Za pomocą tego matematycznego wzoru można wyznaczyć wartości potęgi sumy dwóch liczb. Przydatny jest on w kombinatoryce, tak jak w przypadku silni oraz współczynnika dwumianowego. 

Wzory skróconego mnożenia

To co obowiązkowo trzeba znać i co z pewnością ułatwi rozwiązywanie wielu zadań z matematyki, to wzory skróconego mnożenia. Najogólniej to zbiór wzorów matematycznych, dzięki którym możliwe jest szybsze oraz zdecydowanie łatwiejsze obliczanie iloczynów dwóch lub więcej liczb. 

Najbardziej znanymi wzorami skróconego mnożenia są: kwadrat sumy dwóch liczb, kwadrat różnicy dwóch liczb, iloczyn sumy i różnicy dwóch liczb. Zastosowanie tych wzorów z pewnością skróci czas rozwiązywania zadania, co może być istotne podczas pisania egzaminu maturalnego.

Funkcja kwadratowa

Jest to funkcja matematyczna, którą można zapisać w postaci: f(x) = ax^2 + bx + c. Istotne w funkcji kwadratowej są pewne zależności, które przedstawione są poniżej. Za pomocą tej funkcji można obliczyć punkty przecięcia dwóch krzywych czy obliczyć wartości minimum i maksimum. Wiąże się z nią wzór na deltę (Δ), który obowiązkowo trzeba znać. 

Ciągi

Ciągi to uporządkowany zbiór liczb, które występują w nim w określonej kolejności. Każdy element ciągu określony jest za pomocą wzoru bądź reguły, które warunkują sposób, w jaki kolejne elementy zbioru są tworzone. Wyróżnia się różne rodzaje ciągów, takie jak arytmetyczny, geometryczny czy harmoniczny. Ciągi można zastosować w zadaniach, w których występuje regularność, np. obliczanie n-tego wyrazu ciągu. 

Trygonometria

Trygonometria to jeden z działów matematyki, który zajmuje się badaniem związków i zależności między kątami a długościami boków. W szczególności mowa tutaj o funkcjach trygonometrycznych, którymi są sinus, cosinus i tangens. Opisują one stosunek długości boków trójkąta prostokątnego do kątów pomiędzy nimi. Są to wzory zamieszczone poniżej. 

Za pomocą funkcji trygonometrycznych, z którymi związanych jest wiele wzorów, można obliczyć liczne zadania matematyczne. Dzięki nim można również obliczyć wysokości obiektów, odległości czy kąty padania promieni słonecznych. Funkcje te mają ogrom zastosowań, dlatego warto je znać i potrafić zastosować. 

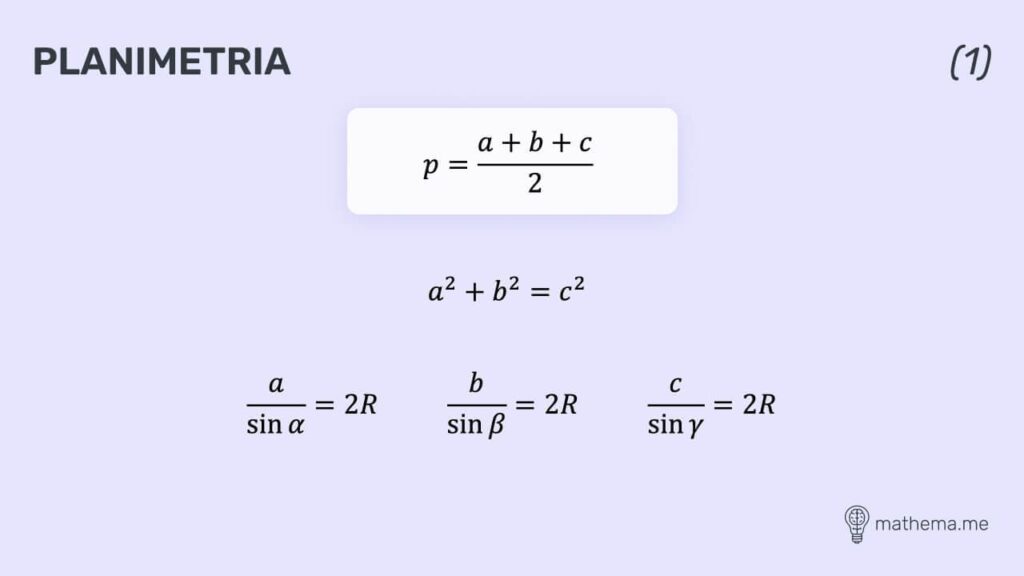
Planimetria

Planimetria zajmuje się badaniem figur płaskich geometrycznych, a więc takich, które posiadają tylko wymiary w postaci długości i szerokości. Mowa tutaj o trójkątach, czworokątach, kołach, wielokątach i innych. Planimetria wykorzystywana jest w wielu dziedzinach nauki oraz życia. 

Niezwykle przydatnymi wzorami są tutaj wzór na pole trójkąta czy podstawowy wzór na twierdzenie Pitagorasa. Poniżej przedstawione są wzory, które potrzebne są do obliczenia pól, wysokości czy obwodów różnych figur geometrycznych. Tutaj również przydatna jest znajomość funkcji trygonometrycznych, pierwiastków, wartości bezwzględnych czy potęg. 

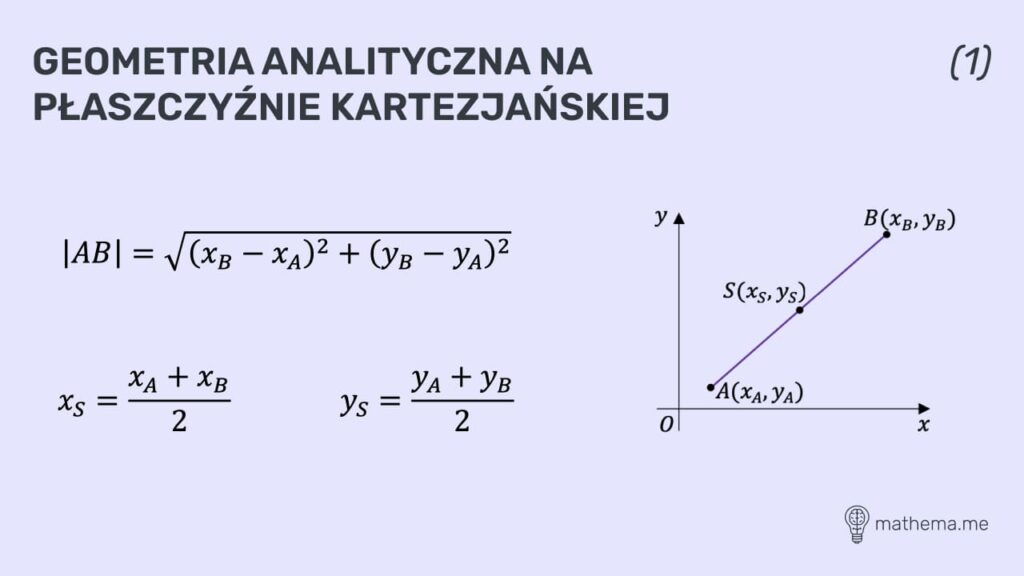
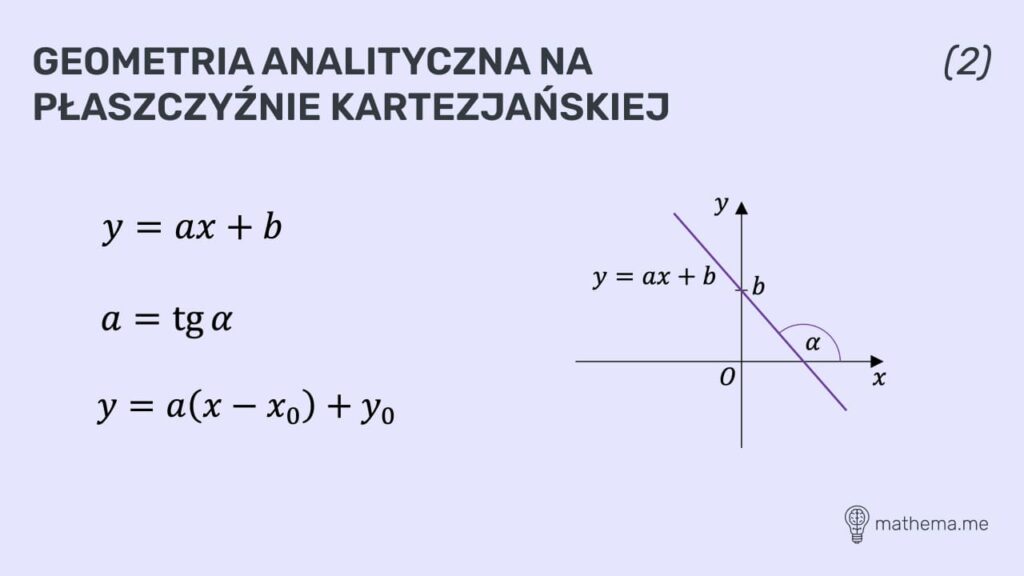
Geometria analityczna na płaszczyźnie kartezjańskiej

Najprościej mówiąc, geometria analityczna na płaszczyźnie kartezjańskiej łączy w sobie geometrię płaską oraz algebrę. Dotyczy ona figur znajdujących się w układzie współrzędnych. Wraz z tym działem matematyki pojawiają się zadania, które polegają na obliczeniu długości danego odcinka czy sformułowaniu wzoru funkcji liniowej przechodzącej przez dwa wskazane punkty.

Stereometria

Jest to kolejny dział geometrii, który zajmuje się figurami, ale w przestrzenii trójwymiarowej. Figury te więc posiadają wymiary: długość, szerokość oraz wysokość. Kluczowe są więc wzory do obliczenia tych parametrów dla sześcianów, prostopadłościanów, stożków, walców, kul i wielu innych. 

Zadania polegają zazwyczaj na obliczaniu, któregoś z tych parametrów bądź na liczeniu objętość lub pola powierzchni. Wszystkie przydatne wzory znajdują się w tym artykule.

Kombinatoryka

Dział matematyki, który zajmuje się badaniem zbiorów i ich właściwości kombinatorycznych, czyli mówiąc prościej, sposobów, za pomocą których można wybierać, ustawiać, permutować i łączyć elementy ze zbioru. Wymienia się tutaj kombinacje,wariacje, permutacje, aranżacje i wiele innych. 

Kombinatoryka może posłużyć do określenia liczby możliwych rozdań kart w grze, liczbę sekwencji liter w kodach lub słowach czy liczbę sposobów ustawienia ludzi w kolejce. Jest przedmiotem wielu zadań na egzaminie maturalny

Rachunek prawdopodobieństwa

Rachunek prawdopodobieństwa wiąże się z badaniem zjawisk losowych oraz szans wystąpienia zdarzeń losowych. Ten dział matematyki określa miarę wystąpienia określonego zdarzenia losowego, jakim jest rzut monetą, rzut kostką, losowanie kul z urny i wiele innych. Poniżej przedstawione są wzory, które stanowią podstawę do obliczenia rachunku prawdopodobieństwa. 

Parametry danych statystycznych

Parametry danych statystycznych to wartości liczbowe, za pomocą których opisywane są charakterystyki określonej zbiorowości danych. Dzięki nim można opisać takie cechy jak na przykład asymetria. Najważniejszymi parametrami danych statystycznych są: średnia arytmetyczna, mediana, wariancja czy  odchylenie standardowe. Są to parametry ważne przy analizie statystycznej.

Pochodna funkcji

Pojęcie pochodnej funkcji pozwala na opisanie jak szybko oraz w jakim kierunku zmienia się wartość funkcji w danym punkcie. Wzór na pochodną funkcji zależy od postaci funkcji. Pochodna funkcji umożliwia łatwe prześledzenie jej zmian.

Przedstawione wzory to wiedza, którą należy posiadać, podchodząc do egzaminu maturalnego. Warto zauważyć, że znajomość samych wzorów matematycznych nie wystarczy na maturze – ważne jest również zrozumienie ich zastosowania i umiejętność ich wykorzystania w rozwiązywaniu konkretnych zadań. 

Na maturze każdy z maturzystów posiada karty maturalne matematyka więc jest do napisania na egzaminie! Warto zapoznać się z powyższymi wzorami. Powodzenia na maturze!