Як розв’язувати рівняння з параметрами на НМТ? Приклади та поради

Цього року до завдань НМТ з математики внесуть рівняння з параметром. Ця новина  налякала багатьох абітурієнтів, які вважають цю тему складною. Однак завдань з розгорнутою відповіддю у мультитесті не буде, а тому і самі рівняння будуть простішими, ніж у ЗНО 2019-2021 років. Mathema розібрала один приклад рівняння з параметром та пояснює як їх розвʼязувати.

Як розв’язати рівняння з параметром? 

Учню потрібно знайти всі значення параметра, при якому рівняння має розв’язок. При одних значень параметра рівняння може не мати розв’язків взагалі, при інших — мати нескінченну кількість. І всі ці випадки потрібно дослідити.

Яку послідовність кроків потрібно виконати, щоб розв’язати такі рівняння ?

1. Знайти область допустимих значень змінної та параметра. Це всі значення “X”, при яких рівняння або нерівність можна розвʼязати.
2. Виразити змінну через параметри.
3. Для кожного допустимого значення параметра знайти множину значень рівняння.

Які бувають типи завдань з параметрами

1. На знаходження  значень  параметра,  при  яких рівняння  має  розв’язки;
2. На знаходження  значень  параметра,  при  яких  рівняння  має певну кількість  розв’язків;
3. На знаходження  значень  параметра,  при  яких  розв’язки  рівняння задовольняють  вказану  умову.

Способи розвʼязань рівняння з параметром

Існує два способи розвʼязання рівнянь за параметром: розрахунковий та графічний. Проаналізувавши завдання, які пропонують цього року у своїх збірниках різні автори, можна зробити висновок, що більшість завдань можна розв’язати графічно.

Наведемо приклад: скільки розв’язків, залежно від значення а, має система рівнянь при:

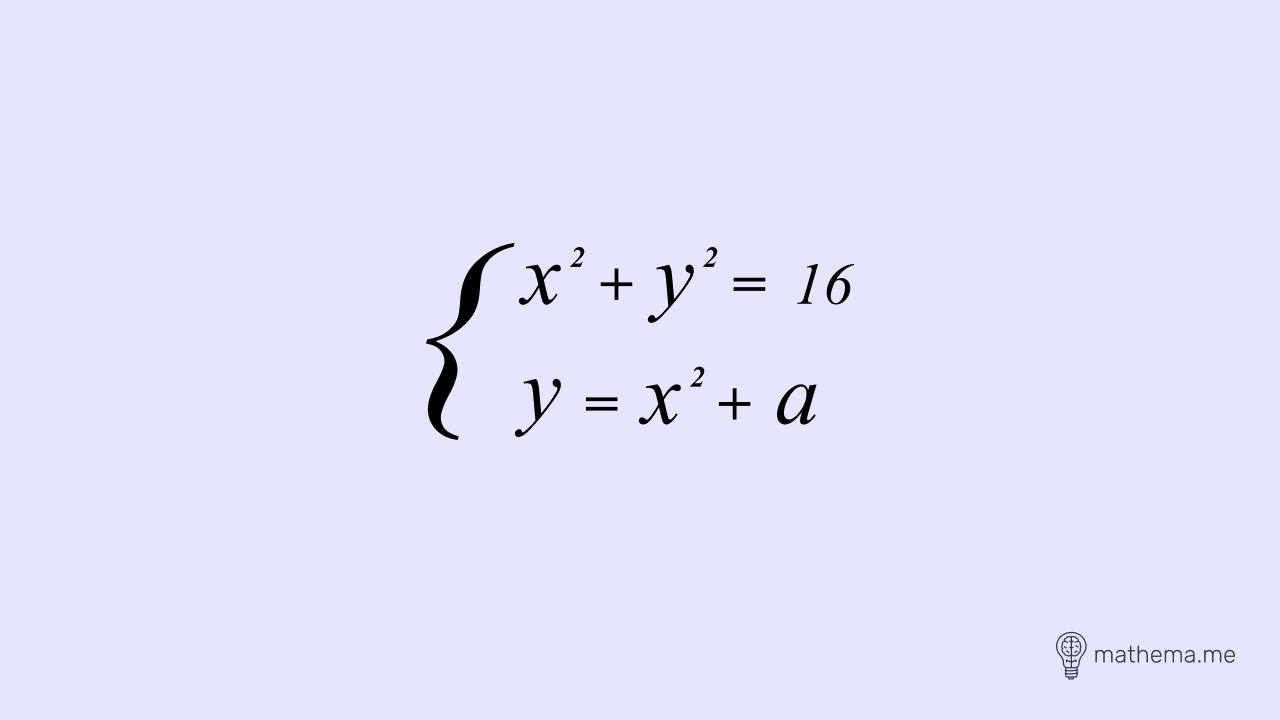
Побудуємо графіки функцій, які входять у систему рівнянь. Перша функція описує коло з центром у точці (0;0) і радіусом 4. Друга — парабола, зміщена по осі “ОX” на “а” одиниць.

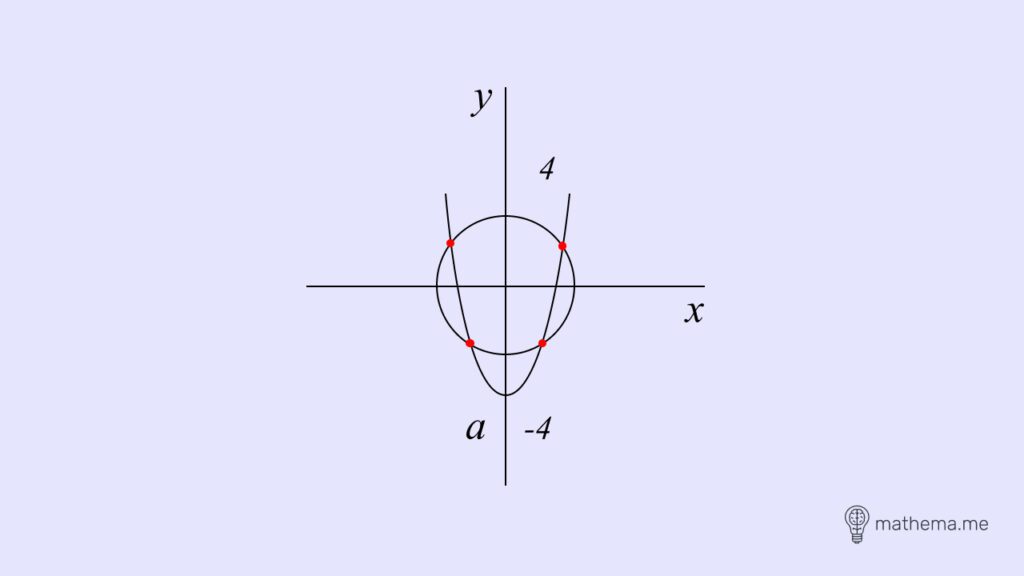
При “а < -4” парабола перетинає коло у чотирьох точках. Отже, рівняння має 4 розв’язки.

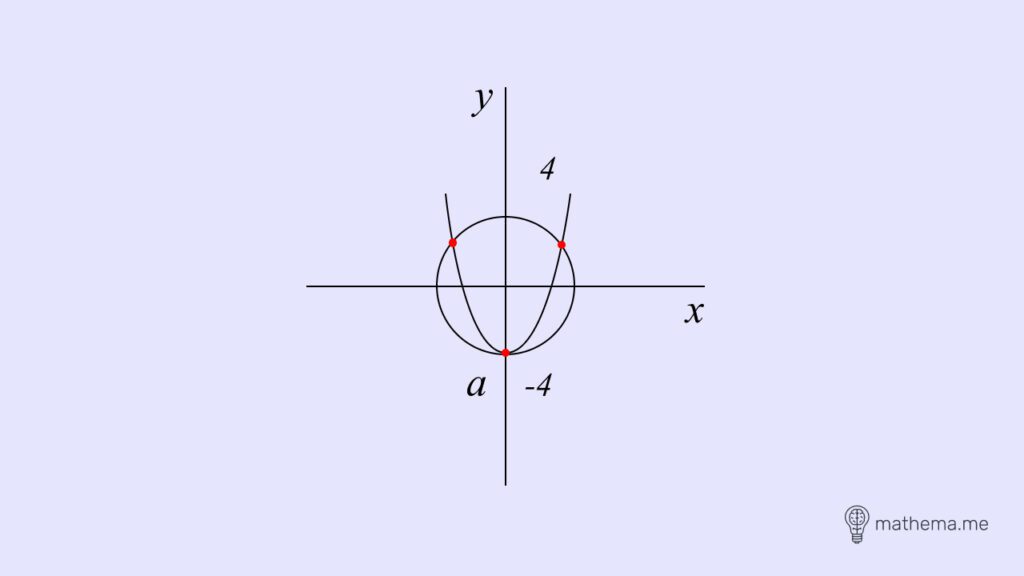
При “а = -4” парабола перетинає коло у трьох точках. Отже, рівняння має 3 розв’язки.

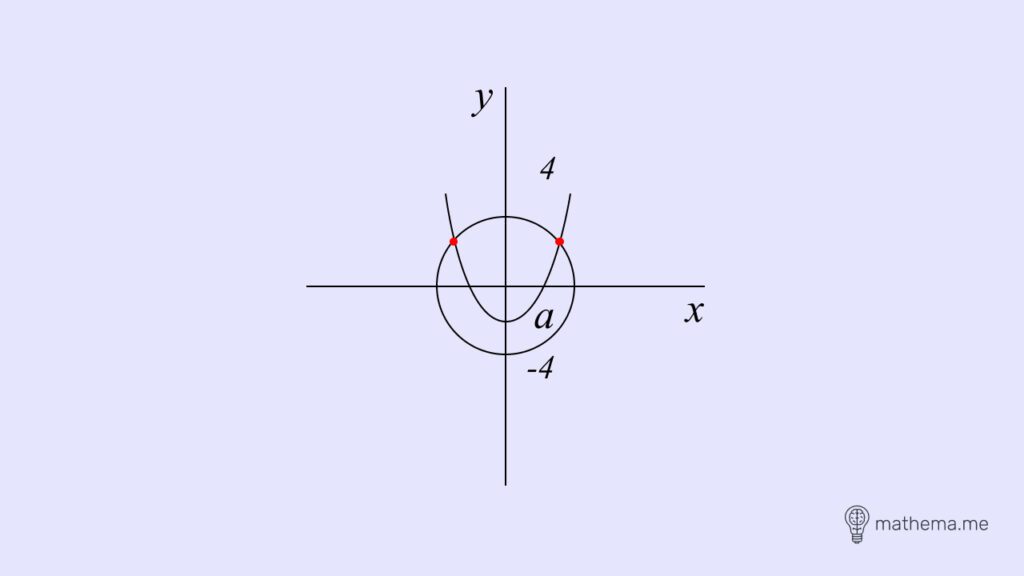
При “-4 < a <4” парабола перетинає коло у двох точках. Отже, рівняння має 2 розв’язки.

При “а = 4”  парабола перетинає коло в одній точці. Отже, рівняння має 1 розв’язок.

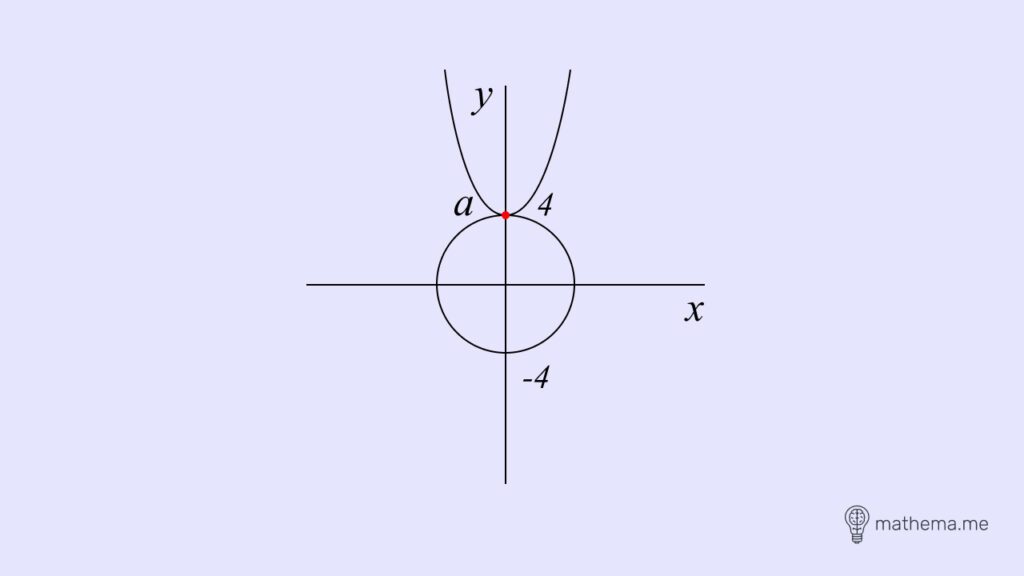
При “а > 4”  парабола не має з колом жодної спільної точки. Отже, рівняння не має  розв’язків.

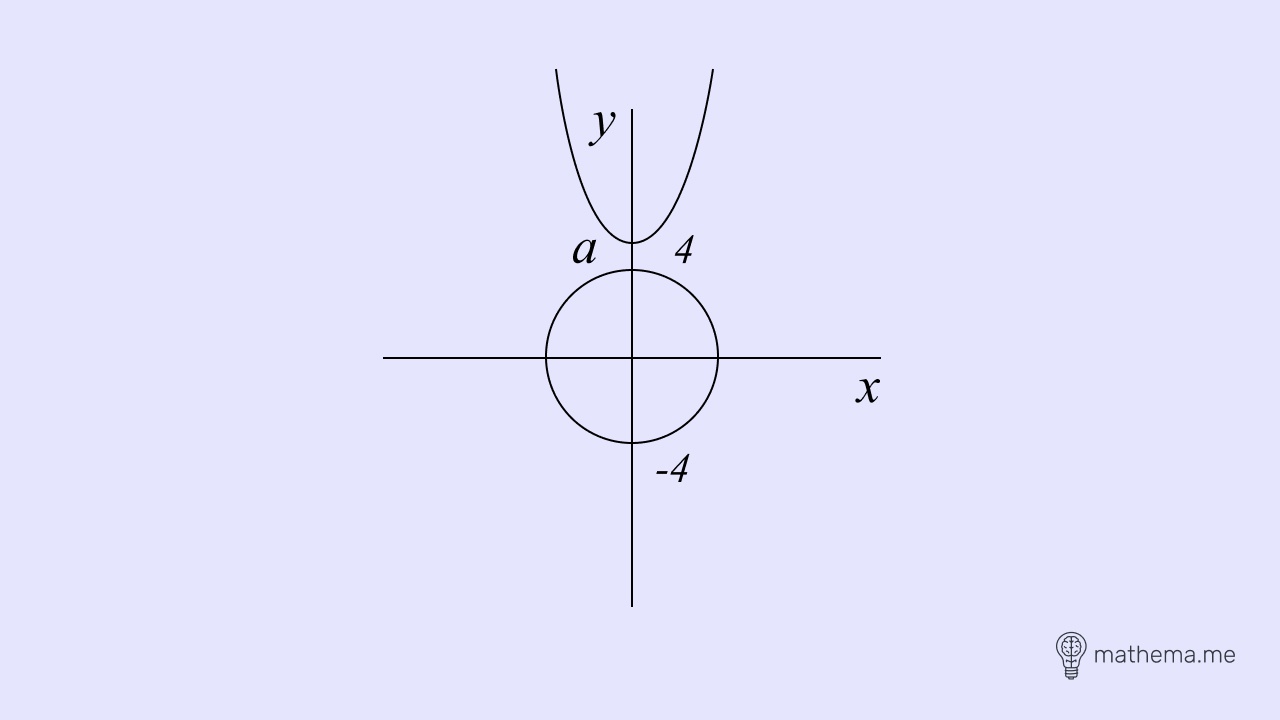
У Демонстраційному варіанті НМТ з математики 2024 року завдань з параметрами немає, проте наші репетитори, при підготовці учнів, акцентують увагу на цій темі. Радимо вам поглиблено ознайомитись з нею, щоб успішно скласти іспит.