Освітня платформа Mathema підготувала розбір демонстраційного тесту НМТ з математики. Репетиторка Mathema Юлія Баганюк розвʼязала усі завдання та розібрала найскладніші моменти тесту. Матеріал створений для абітурієнтів, які готуються до НМТ з математики. Він допоможе проаналізувати завдання та перевірити власні помилки.
Завдання 1
Щоб розв’язати цю задачу, потрібно знати, як додавати числа та розуміти, що “на 17 більше” означає додавання числа 17.
У першу годину надійшло 145 дзвінків.
У другу годину надійшло на 17 дзвінків більше, тобто: 145 + 17 = 162.
Тепер, щоб знайти загальну кількість дзвінків за дві години, додамо кількість дзвінків у першу і другу годину:
145 (дзвінків у першу годину) + 162 (дзвінків у другу годину) = 307.
Отже, загальна кількість дзвінків за дві години роботи гарячої лінії – 307.
Відповідь: А
Завдання 2
Щоб знайти значення x, слід розуміти, що середнє арифметичне чисел обчислюється як сума всіх чисел, поділена на їхню кількість. В задачі дано середнє арифметичне (3,5 градусів) і кількість метеостанцій для кожної температури. Ми можемо використати ці дані і скласти рівняння.
Спочатку визначимо суму всіх температур, помножених на їхню кількість:
1⋅2+3⋅3+4⋅4+х⋅1
Тепер поділимо цю суму на загальну кількість метеостанцій:
Ми знаємо, що середнє арифметичне дорівнює 3,5 градусів, отже ми можемо записати рівняння і розв’язати його:
2+9+16+x=3,5⋅10
27+х=35
27+x=35
х=35−27
x=35−27
х=8
Отже, х=8.
Відповідь: Г
Завдання 3
Бічною гранню прямої трикутної призми є прямоутник.
Відповідь:Б
Завдання 4
Підставимо у вираз 7-m значення n-1, отримаємо
7-(n-1)
Вираз n-1 потрібно взяти в дужки, оскільки ми маємо “- “ перед m, отже потрібно від 7 відняти весь вираз n-1.
Далі розкриваємо дужки змінюючи знаки на протилежні і зводимо подібні доданки:
7-n+1=8-n
Відповідь: В
Завдання 5
На малюнку проведемо радіуси двох кіл
ОА – це радіус великого кола і він рівний 12 см.
О1А – радіус малого кола. О1А=8 см.
На малюнку видно, що радіус великого кола ОА складається з двох відрізків ОО1 та О1А. Можемо записати:
ОА= ОО1 +О1А. Звідси ми отримаємо, що шуканий відрізок ОО1=ОА-О1А. Підставимо відомі значення радіусів і обчислимо довжину ОО1
ОО1=12-8=4 (см)
Відповідь: Г
Завдання 6
Дана нерівність є лінійною, оскільки х знаходиться в першому степені. Перенесемо відомі в праву частину нерівності, а невідомі залишимо в лівій. Отримаємо:
0,2х<54
Поділимо обидві частини нерівності на коефіцієнт біля х, тобто 0,2. При цьому знак нерівності залишаємо той самий, оскільки 0,2>0.
х<54:0,2
х<270
Отже, розв’язком нерівності є всі числа менші за 270. Запишемо це у вигляді проміжку (-∞;270). Проміжок запишемо в круглих дужках, оскільки нерівність строга, а отже 270 не включаємо в проміжок.
Відповідь: А
Завдання 7
Нулями функціями називають такі значення аргументу, при яких значення функції дорівнюють нулю. Тобто це ті значення, в яких у=0. На графіку це точки в яких графік функції перетинає вісь Ох.
На рисунку графік перетинає вісь Ох в одній точці, отже функція матиме один нуль.
Відповідь: Б
Завдання 8
Розкриємо дужки у виразі, застосовуючи до (а+b)2 формулу скороченого множення квадрат різниці (формула є в додатку до НМТ) та враховуючи – перед другою дужкою:
a2+2аb-a2-2ab-b2
Зведемо подібні доданки і отримаємо: -b2
Відповідь: В
Завдання 9
Побудуємо цей трикутник.
Кут В – тупий, отже він більше 90 градусів. Оскільки, сума всіх кутів трикутника рівна 180 градусів і кут В більший 90 градусів, то сума кутів А і С буде менша 90 градусів, отже, перше твердження вірне.
Пригадаємо умову існування трикутника: трикутник існує тоді і тільки тоді, коли сума будь-яких двох його сторін більша третьої сторони. Друге твердження суперечить цій умові, а, отже, є неправильним.
Третє твердження є вірним, оскільки дійсно центр кола описаного навколо тупокутного трикутника буде лежати поза цим трикутником.
Отже, правильні твердження І, ІІІ
Відповідь: Д
Завдання 10
Розлянемо вираз |а-1| . Оскільки згідно умови а<1, тоді вираз а-1 завжди буде менше за 0 (наприклад: нехай а=0, 0-1=-1, -1<0).
Аналогічно |-7|. -7<0, тобто і в другому модулі підмодульний вираз теж менший за нуль.
Пригадаємо означення модуля (є в додатках до НМТ):
Оскільки у завданні обидва підмодульні вирази від’ємні, то ми розкриваючи знак модуля, змінюючи у підмодульних виразах знаки на протилежні. Отримаємо:
|а-1|+|-7|=-а+1+7=-а+8 .
Відповідь: Д
Завдання 11
Проаналізуємо кожне рівняння системи.
Перше рівняння системи лінійне, друге – показникове.
Розв’яжемо спочатку друге рівняння. Справа 16 ми можемо записати як 42. Таким чином наше рівняння матиме вигляд:
Застосуємо властивість степеня до правої частини і отримаємо:
Таким чином ми отримали однакові основи, а отже можемо прирівняти показники степеня.
Друге рівняння системи розв’язали і отримали, що х=-2. Можемо підставити отримане значення х в перше рівняння і знайти чому рівний у.
-2+у=5
у=5+2
у=7
Оскільки в умові завдання нам потрібно знайти добуток отриманих розв’язків, помножимо -2 на 7
-2*7=-14
Відповідь: Б
Завдання 12
Правильна чотирикутна піраміда – це піраміда, в основі якої лежить квадрат і вершина проектується в центр вписаного і описаного кіл. Побудуємо дану піраміду і проведемо в ній апофему (висота бічної грані) і висоту.
SK- апофема. SK=15 см.
SO – висота піраміди.
Отриманий трикутник SOK – прямокутний, оскільки SO-висота, а отже вона перпендикулярна основі (кут SOK=90о). Згідно теореми Піфагора:
ОК-це радіус вписаного кола в квадрат АВCD, а отже ОК=ВС/2
Сторону квадрата ВС можемо знайти з периметра.
РАBCD=4 *ВС=72 звідси ВС=72/4=18 (см). Отже ОК= 18/2=9 (см)
Підставимо відомі величини і знайдемо висоту SO:
Відповідь: Г
Завдання 13
Дане рівняння є найпростішим логарифмічним рівнянням. Щоб розв‘язати рівняння пригадаємо означення логарифма: логарифм – це показник до якого потрібно піднести основу, щоб отримати підлогарифмічний вираз. Використавши означення матимемо:
Застосувавши властивість степеня з від’ємним показником 
Число 8 потрапляє в проміжок (7;9⦎
Відповідь: Д
Завдання 14
Розглянемо трикутник АВD:
Застосуємо до трикутника ABD теорему синусів (є в додатках НМТ):
За правилом пропорції:
Відповідь: Д
Завдання 15
Розкриємо дужки:
Оскільки ми отримали суму двох функцій х4 та х, застосуємо правила знаходження похідної від суми
і знайдемо похідні використовуючи таблицю похідних (є в додатках НМТ). Матимемо:
Відповідь: А
Завдання 16
1. Функція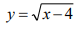 
не визначена в точці х=1.
Підставимо у функцію замість х значення 1, матимемо:
Під коренем ми отримали -3, що не не належить області визначення (корінь квадратний з від’ємного числа не існує).
Відповідь: Б
2. Побудуємо графік функції у=2
Графіком є пряма паралельна осі Ох, яка перетинає вісь Оу в значенні у=2.
На графіку видно, що при значенні х=-3 функція набуватиме додатного значення.
Відповідь: Г
3. Перевіримо дану функцію на парність підставивши у функцію замість -х
(властивість парних і непарних функцій )
Отже функція непарна.
Відповідь: Д
Завдання 17
Вираз 1
Використаємо властивість про ділення степенів з однаковими основами (є в додатках НМТ). Оскільки основи однакові, залишаємо основу ту ж саму. а показники віднімаємо. Отримаємо:
Відповідь: Д
Вираз 2
Розкладемо чисельник дробу на множники, винісши а за дужки:
Винесемо в знаменнику за дужки -1. Таким чином ми отримаємо однакові множники (а-1) в чисельнику і знаменнику, які можна скоротити.
Відповідь: Г
Вираз 3
Даний в умові вираз логарифмічний. Внесемо знак – перед логарифмом в підлогарифмічний вираз використавши властивість логарифма (є в додатках НМТ)
Отримаємо:
Застосуємо основну логарифмічну тотожність 
Відповідь: В
Завдання 18
Відрізок 1
Площа квадрата рівна стороні квадрата помноженій самій на себе і рівна 36 см2 за умовою.
Звідси можемо знайти а добувши корінь з 36.
Відповідь: Г
Відрізок 2
Оскільки трапеція BMNC – прямокутна, то висотою є сторона ВМ.
Розглянемо відрізок АМ
АМ=ВМ+АВ=15см. Звідси ВМ=АМ-АВ=15-6=9 (см) (сторону АВ ми знайшли в попередньому пункті завдання)
Відповідь: Д
Відрізок 3
Менша основа трапеції – це МN. Запишемо формулу для знаходження площі даної трапеції (є в додатках НМТ)
де ВС, MN – основи, BM- висота.
Підставивши відомі дані в формулу, отримаємо рівняння з невідомим MN
Розв’яжемо рівняння і знайдемо довжину основи MN.
Відповідь: А
Завдання 19
Для розв’язання цієї задачі потрібно використати знання з теми “Числові послідовності”.
Оскільки в кожному наступному ряду (починаючи зверху) на одну колоду більше, то числа які відображають кількість колод в кожному ряду є членами арифметичної прогресії.
Нам відомо, що у верхньому ряду одна колода. отже а1=1, а у нижньому – 13, тобто аn=13. Різниця d арифметичної прогресії рівна 1, оскільки вказано. що в кожному наступному ряду на одну колоду більше.
Щоб знайти загальну кількість колод потрібно знайти суму n перших членів арифметичної прогресії. Запишемо формулу для знаходження суми (є в додатках НМТ):
З умови задачі n (кількість членів арифметично прогресії)=13
Підставимо дані у формулу і знайдемо суму:
Відповідь: 91.
Завдання 20
Це завдання з теми “ Комбінаторика”. Розгляньмо умову задачі:
- Є 6 різних новин: 2 політичні, 3 суспільні та 1 спортивна.
- Політичні новини повинні бути на початку.
- Спортивна новина повинна бути останньою.
Розгляньмо, скільки можливостей для розміщення політичних новин. Позначимо їх як P1 та P2:
- P1 може займати перше місце, і P2 може займати друге місце.
- P2 може займати перше місце, і P1 може займати друге місце.
Отже, є 2 можливості для розміщення політичних новин.
Тепер розглянемо розміщення суспільних новин (S1, S2, S3) після політичних новин. Ми маємо 3 новини, тому можливостей для їх розміщення буде 3! (3 факторіал).
Нарешті, спортивна новина (S) має зайняти останнє місце.
Отже, загальна кількість можливих послідовностей:
2*3!=2*6=12
2*3!=2*6=12
Отже, є 12 різних послідовностей розміщення цих 6 новин.
Відповідь: 12.
Завдання 21
Скалярний добуток двох векторів OA і AB обчислюється за формулою (є в додатках НМТ):
де (а1,а2,а3) – координати першого вектора, (b1,b2,b3) – координати другого вектора.
Координати вектора АВ відомі. Знайдемо координати вектора ОА.
Оскільки т. О – початок координат, то т. О має координати (0;0;0).
Знайдемо координати т.А (х1,у2,z3) використовуючи вектор АВ. для цього використаємо формулу знаходження координат вектора (є в додатках НМТ).
Звідси знайдемо координати т.А
Отже, т. А (10;-10;-1)
Знайдемо координати вектора ОА, для цього координат кінця вектора віднімаємо координати початку. Оскільки т.О має координати (0;0;0) то координати вектора ОА співпадатимуть з координатами т.А
Знайдемо скалярний добуток векторів ОА та АВ
Відповідь: -111
Завдання 22
Оскільки область значення функції синус – від -1 до 1,
і якщо до аргументу додати П/3 то графік функції рухатиметься по осі Ох, тобто значення функції змінюватись не буде
Запишемо дану подвійну нерівність у вигляді системи
Розв’яжемо кожну нерівність системи окремо
1-ша нерівність
Запишемо відповідну квадратичну функцію
Графіком цієї функції є парабола вітки якої напрямлені вгору, оскільки біля а2 коефіцієнт більший 0. Знайдемо нулі функції, для цього прирівняємо її до 0 і розв’яжемо отримане квадратне рівняння:
2-га нерівність
Графіком цієї функції також є парабола вітки якої напрямлені вгору, оскільки біля а2 коефіцієнт більший 0. Знайдемо нулі функції, для цього прирівняємо її до 0 і розв’яжемо отримане квадратне рівняння:
Зобразимо на числовій прямій всі отримані розв’язки обох нерівностей і позначимо відповідні проміжки
Розв’язком системи будуть ті проміжки, на яких перетинаються проміжки розв’язків обох нерівностей. Оскільки нас цікавить найменше значення а, то розглянемо проміжок [-3,5;-3,25]. Найменшим значенням на цьому проміжку є -3,5.
Відповідь: -3,5.
